Monthly Archives: July 2020

Linear Algebra exercises.

Posted on by
Reply
  1. What’s eigenvalues of a n\times n matrix A=\begin{pmatrix} 1 & c & c & \dots & c\\ c & 1 & c & \dots & c\\ c & \vdots &\vdots && \vdots \\ \vdots &\vdots & & 1&c\\ c&c&c\dots&c&1\end{pmatrix} ?

Solution 1: Notice that A=c J+(1-c)I, where I,J are identity and ones matrix respectively. Assume v is an eigen-vector associated with an eigen-value \lambda, then

\begin{aligned} &&cJv+(1-c)Iv=\lambda v\\ &\implies& c|v|\overset{\rightarrow}{1}=(\lambda+c-1) v. \end{aligned}

Therefore,  v=\overset{\rightarrow}{1} , when  c|v|=(\lambda+c-1), i.e., \lambda_1=1+(n-1)c.

Otherwise, |v|=0 when \lambda_{2,\dots,n}=1-c, this is a n-1 dimension subspace \text{span}\{\begin{pmatrix} 1\\,-1\\, 0\\, \vdots,\\0\end{pmatrix}, \begin{pmatrix} 1\\,0\\, -1\\, \vdots,\\0\end{pmatrix}, \dots, \begin{pmatrix} 1\\,0\\, 0\\, \vdots,\\-1\end{pmatrix}\}.

 

Solution 2: Matrix Determinant lemma (wikipedia: https://en.wikipedia.org/wiki/Matrix_determinant_lemma#Proof)

Statement: \text{det} (A+uv^T)=(1+v^TA^{-1}u)\text{det}(A), where A is an invertible matrix, u,v\in \mathbb{R}^{n,1}.

Let’s denote A=(1-c-\lambda)I_{n,n}, and u,v=\sqrt c \overset{\rightarrow}{1}_{n,1}, we can solve the eigenvalue from the corresponding polynomial

\begin{aligned} (1+\frac{c}{1-c-\lambda}\cdot n)(1-c-\lambda)^n=(1-\lambda+(n-1)c)(1-c-\lambda)^{n-1} \end{aligned}.

Therefore, the eigenvalues \lambda_1=1+(n-1)c, \lambda_{2,\dots,n}=1-c.

Monte Hall problem revisit

Posted on by
Reply

This post is to write the Bayesian proof of the monte hall goat problem. Below is the statement of the problem from wikipedia:

Suppose you’re on a game show, and you’re given the choice of three doors: Behind one door is a car; behind the others, goats. You pick a door, say No. 1, and the host, who knows what’s behind the doors, opens another door, say No. 3, which has a goat. He then says to you, “Do you want to pick door No. 2?” Is it to your advantage to switch your choice?

Analysis: the answer to this question is depending on whether you’re a Bayesian or a frequentist. Although the former is the approach through which the answer is widely known (with hidden assumptions such as the host is randomly choosing between the rest doors if your first guess is correct).

Bayesian:

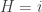Denote {C=i} as event that the car is behind the door i, {I=i} as event of your first guess, {H=i} as event that the host opened the door i with a goat behind. Hence,

\begin{aligned} P(C=2|I=1,H=3) &=\frac{P(I=1,H=3|C=2)*P(C=2)}{P(I=1,H=3|C=1)*P(C=1)+P(I=1,H=3|C=2)*P(C=2)+P(I=1,H=3|C=3)*P(C=3)}\\ &=\frac{1*\frac{1}{3}}{\frac{1}{2}*\frac{1}{3}+1*\frac{1}{3}+0*\frac{1}{3}}\\ &=2/3 \end{aligned}

Meanwhile ,P(C=1|I=1,H=3)=\frac{1}{3}. Therefore, the correct choice is to switch your decision from door 1 to door 2.

Frequentist:

However, as a frequentist, there is no prior distribution. This approach would draw the inference as below:

Assume, 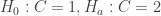H_0: C=1, H_a: C=2, then

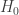P_{H_0}(H=3)=\frac{1}{2} is a big number, therefore, we’re not able to reject H_0. Vice Versa for H_a.

Unfortunately, frequentist is not able to answer the question of posterior probability so it’s not able to answer the question whether switch or not.